


Next: The Butterfly Up: The Lasso Previous: Flat Loop Tricks
Please Read The Copyright Notice




Next: The Butterfly
Up: The Lasso
Previous: Flat Loop Tricks
Amongst the most impressive rope tricks for a general audience is the Texas Skip. If you tell your friends that you are working on trick roping they'll want to know if you can jump through a vertical loop. Well, the good news is that learning to make a Vertical Loop is perhaps easier than learning the Flat Loop. The Texas Skip, which is a Vertical Loop that you pull back and forth while jumping through the loop, takes a little work but is far from being a difficult trick. If you learned the Flat Loop, folks, you can learn this one and it will be one of the best tricks in your repertoire.
To do the Texas Skip you first have to master the Vertical Loop. As already stated the Vertical Loop is easy to learn, nevertheless, it is essential to have the right equipment. The following sections describe how to make a lasso for the Vertical Loop; how the Vertical Loop is done; how to do the Texas Skip; and, finally, for those of you who are scientifically inclined, a section on how to calculate the exact weight of the honda for the Vertical Loop. This last section is unnecessary for learning lasso tricks but is included in this book for ``sentimental'' reasons.
The lasso used for the Vertical Loop and the Texas Skip is not the same
lasso used for flat loop tricks. First, the
Vertical Loop lasso is longer than a Flat Loop lasso. The length
of a Vertical Loop lasso
varies according to the height of the user, a nominal
length is about 24 feet (7.4 meters). A rough
calculation of the minimum length necessary for a Vertical Loop rope
is made by calculating the perimeter of a circle
of diameter equal to the height of the roper
plus a spoke length of half the diameter. The formula for this calculation is
length = 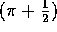
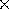 height of person
where
height of person
where 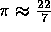 . For example, someone who is 6 feet tall
would need a rope at least 22 feet long. I'm only 5 feet 8 inches tall,
however, and I use a rope 24 feet long for the Vertical Loop.
In any case a little extra cord is usually a good idea and can't
hurt since the excess cord can be coiled up in the hand.
Confucius says: ``A rope that is too long can always be cut down but a rope that
is too short can never be lengthened!''
. For example, someone who is 6 feet tall
would need a rope at least 22 feet long. I'm only 5 feet 8 inches tall,
however, and I use a rope 24 feet long for the Vertical Loop.
In any case a little extra cord is usually a good idea and can't
hurt since the excess cord can be coiled up in the hand.
Confucius says: ``A rope that is too long can always be cut down but a rope that
is too short can never be lengthened!''
An essential part of the Vertical Loop rope is the honda weight. For a Vertical Loop rope to work correctly, the honda must be weighted to balance the opening force of the spinning loop. If the honda is too light the loop diameter of the Vertical Loop will grow too large and if it is too heavy the loop diameter will become too small. There was a time when brass hondas were specially fabricated for Vertical Loop and Texas Skip lassos. These hondas essentially had the correct weight and this weight could be adjusted by filing the honda to make it lighter or by wrapping wire around the honda base to make it heavier. Unfortunately, these brass hondas are very difficult to come by but there are two potential sources. The first is with Mark Allen Productions [9] who is the biggest distributor of roping equipment that I know of (ropes, books, and videos) and the second is with the juggling manufacturer Brian Dube, Inc [1] . Both of these companies distribute brass hondas for the Vertical Loop.
In any case, a very serviceable metal honda can be improvised with a
piece of marine hardware called a sailing thimble .
Sailing thimbles are used for finishing cables and lines
on boats and are available in a variety of sizes, weights, and
materials from marine hardware stores. The stainless steel varieties are
probably the most suitable for rope spinning. The big question
is what weight thimble should be used for the
Vertical Loop. The answer to this question depends
both on the linear density of the rope and on
the desired diameter of the Vertical Loop to be spun.
The formula for calculating the
correct honda weight is 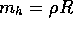 where
where 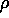 is
the linear density of the cord used, R is the desired radius
of the Vertical Loop, and
is
the linear density of the cord used, R is the desired radius
of the Vertical Loop, and 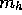 is the resulting honda mass required for this
rope (see Section 3.4 for the physical derivation of this formula).
is the resulting honda mass required for this
rope (see Section 3.4 for the physical derivation of this formula).
To obtain the linear density of the
rope used, weigh your Vertical Loop rope (without the honda, of course)
and divide its weight by its length (for example, if the
rope weighs 336 grams and the length of the cord is 24 feet then the
linear density of this cord is 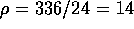 gr./ft.). If
you don't have a scale, bring your rope to the post
office and ask to have it weighed there. For nylon core #10 Samson spot cord
[13] (which is what I use), the nominal honda weight for a 24 foot cord
should be about 40 grams (1.41 oz.) and for #12
Samson spot cord it should be about 55 grams (1.94 oz.). In any case
it will probably be necessary to obtain a number of sailing thimbles
of varying weights and to
experiment a bit. If a sailing thimble with the correct
weight cannot be found choose a thimble which is lighter than the
required weight and then wrap copper wire
around the honda base to obtain the weight desired.
Once you've sewn the end of your Vertical Loop rope around the
sailing thimble (see description in Section 1.1) and adjusted the
weight, if necessary, with additional copper wire you are ready to start learning
the Vertical Loop.
gr./ft.). If
you don't have a scale, bring your rope to the post
office and ask to have it weighed there. For nylon core #10 Samson spot cord
[13] (which is what I use), the nominal honda weight for a 24 foot cord
should be about 40 grams (1.41 oz.) and for #12
Samson spot cord it should be about 55 grams (1.94 oz.). In any case
it will probably be necessary to obtain a number of sailing thimbles
of varying weights and to
experiment a bit. If a sailing thimble with the correct
weight cannot be found choose a thimble which is lighter than the
required weight and then wrap copper wire
around the honda base to obtain the weight desired.
Once you've sewn the end of your Vertical Loop rope around the
sailing thimble (see description in Section 1.1) and adjusted the
weight, if necessary, with additional copper wire you are ready to start learning
the Vertical Loop.
The Vertical Loop must be mastered before the Texas Skip. It's not a very difficult trick and, in fact, someone with no experience with rope spinning can often succeed in a few tries at sustaining a Vertical Loop when it is started and passed from the hands of an experienced rope spinner. It is a little tricky, however, to start the Vertical Loop. The starting configuration of the hands is identical to that used for the Flat Loop (depicted in Figure 1.3) except that now the spoke length should be about half the length of the desired loop diameter. This is in contrast to the spoke length for the Flat Loop which must be between a quarter and a fifth of the loop circumference.
You'll have a much easier time of learning how to start the Vertical Loop if you keep in mind the following facts. First, you want to spin a loop in the vertical plane with a loop that has a diameter equal to the height of the roper. Consequently, you must remember to keep the hand which is holding the spoke sufficiently elevated to keep the loop from touching the ground. Second, as described in Section 1.4, it is important to remember that there must be a quarter circle phase difference between the hand and the honda. Third, the spoke of the Vertical Loop is in the plane of the loop itself which is an important difference between this trick and the Flat Loop. Finally, The force that the hand applies to the end of the spoke is not uniform as in the case of the Flat Loop.
To better understand the action of the force applied to the spoke imagine a small weight attached to the end of a piece of cord. To make the weight describe a circle in the vertical plane one needs to accelerate the weight (i.e., apply force to the end of the cord) while the weight is in the lower half of its circle. If enough force is given in the lower half of the circle the weight will continue through the upper half of the circle without falling prematurely. In the upper half of the circle the hand continues to apply some force to the end of the cord to prevent the weight from flying away, however, the hand needn't accelerate the weight in the same way. Although the force applied by the hand to the end of the spoke is not identical to that for the weight at the end of a cord, it is very similar in feel and a useful image to keep in mind.
With the preceding description in mind, it is necessary to go from the starting configuration to successfully spinning the Vertical Loop. The position of the Vertical Loop can be in front of or on the right hand side of the body. The Vertical Loop turns in the clockwise direction from the point of view of the roper (see Figure 3.1(a)). Hold the rope as in Figure 1.3 with the honda hanging down from the right hand on the right side of the loop. Treating the honda as the weight on the end of the cord in the preceding description swing the honda from 6 o'clock through 9 o'clock with enough force so that the honda and the rest of the rope in the loop will follow the honda up through 12 o'clock and around through 3 o'clock without falling prematurely.
To perform this start with the Vertical Loop the right hand pulls the spoke, the honda, and the loop through a large arc traversing about half the circle of the Vertical Loop. Throughout the movement of this half circle the left hand maintains its grip on the loop and assists a bit in obtaining the circular form of the Vertical Loop. After the initial half turn both the left and right hands release the loop and the right hand, maintaining its grip on the spoke, spirals directly into the center of the spinning Vertical Loop. As the right hand spirals in to the center it is essential to keep the quarter circle phase advance principle in mind. Also, It is important to avoid flailing too much with the arm after the initial half turn of the loop. If the initial force given to the mass of the loop is insufficient to keep it going in the first turn the trick will fail regardless of what you do afterwards. Consequently, a large arm movement is necessary to start the Vertical Loop. After the first one half turn, however, the hand basically moves through a circle of about a half foot in diameter. A final reminder is that the Vertical Loop must not touch the ground. Keep your spinning hand up otherwise the loop will scrape against the ground making it impossible to continue.
As with the Flat Loop it is necessary to untwist the spoke for the Vertical Loop (see Section 1.5). Unfortunately, untwisting the spoke of the Vertical Loop is a bit more difficult than for the Flat Loop. Fortunately, with the Texas Skip the twists in the rope are worked out automatically as the Vertical Loop is done first on one side of the body then on the other.
The Texas Skip is a Vertical Loop which is repeatedly pulled from one side of the body to the other and where, for each pass, the roper jumps through the center of the loop. Timing is the key to the Texas Skip and in this respect it is similar to Spoke Jumping (see Section 2.2). For Spoke Jumping you put your foot inside the loop when it won't get in the way of the spoke. For the Texas Skip you pull the Vertical Loop from one side of the body to the other when your body won't get in the way of the spoke. Consequently, the jump is made while the spoke is in the front half of the Vertical Loop.
Figure 3.1 illustrates the correct timing for the jump. Referring to part (a) of the figure you'll see that the Vertical Loop is on the right side of the roper and spinning in the clockwise direction from the roper's point of view. Using spin acceleration to prevent the loop from closing, the roper begins pulling the spoke from the right to the left side of the body when the honda is at the 12 o'clock position. The pull must be timed so that the honda will have just passed the 6 o'clock position when the roper begins to jump. Part (a) of the figure illustrates the moment just before the jump begins. During the jump the roper continues to pull the spoke to the left as the honda passes through the point mid-way between 6 and 12 o'clock as illustrated in Figure 3.1(b). As the jump is completed the loop is now completely on the left side of the roper and the honda is at the 12 o'clock position. The roper then makes one complete circle on the left side of the body (i.e., the honda passes from 12 o'clock to 12 o'clock) with the honda now turning in the counter-clockwise direction.
At this point the entire preceding procedure is repeated but in the reverse direction. Thus, the roper begins to pull the loop back to the right hand side, timing the jump for 6 o'clock. The honda passes the mid-way point between 6 and 12 o'clock at mid-jump and arrives at the 12 o'clock position at the end of the jump. The honda then makes a full circle on the right side of the body to complete the first full cycle of the Texas Skip. The Texas Skip is continued by continuously repeating the preceding description.
An important point to remember is that the roper pulls the spoke across the body, jumping at the appropriate time. This means that the roper remains on the same spot as the loop passes from side to side. Many beginners make the mistake of trying to jump through the loop without moving it (i.e., leaving the loop on the same spot and passing the roper from one side to the other). The essential element for success with the Texas Skip is to pull the Vertical Loop across the body with the appropriate timing.
A complete Texas Skip sequence consists of four turns of the Vertical Loop: a turn on the right side of the roper, a pass of the loop from right to left, a turn on the left side, and a pass back from the left to the right. A nice variation of the Texas Skip can be had by eliminating the turns on the right and left sides. The resulting trick consists of just two turns of the loop: one which passes the loop from right to left and the other which passes it back. This makes for a ``fast'' Texas Skip and it is particularly nice in a routine when it follows a regular Texas Skip.
Another variation on the Texas Skip which is often seen is called the Turn-Around Texas Skip. This is a simple variation where, as the Vertical Loop is being pulled from the right side to the left, the roper turns counter-clockwise from front to back. Now the Vertical Loop is on what was the left side of the roper but because of the counter-clockwise turn is now the right side. From the roper's perspective the rope is now turning in the counter-clockwise direction. The loop makes a full circle on this side of the roper and then is again pulled to the left as the roper once again turns counter-clockwise from front to back. For this pass of the Vertical Loop the honda is turning in the direction opposite that for the normal Texas Skip. As before the timing of the jump must be made to avoid impeding the passage of the spoke. After the jump the loop is once again on the right side of the roper where it is now turning in the clockwise direction. A full turn of the honda on this side completes the description of a full Turn-Around Texas Skip sequence.
From my perspective this section is the most important of this entire book. I say this not because there is anything in it that will help you learn more about trick roping but because if I hadn't had problems discovering the correct weight of the honda for the Vertical Loop I probably never would have written this book.
Discovering the correct honda weight is easy when you already know how to do a Vertical Loop. All you need to do is to iteratively try the trick with different honda weights until it works correctly. At the beginning, however, I didn't know how to do the Vertical Loop. My problem was that I didn't know whether it wasn't working because I was doing it wrong or because I didn't have the correct weight! I felt that I needed to get an independent, theoretical value for the honda weight before I could work effectively on learning the Vertical Loop.
Once I had theoretically determined the correct honda weight and had verified this calculation by experimental tries in the laboratory I wanted to share this discovery with others. One thing leads to another and as I started to teach others different types of lasso tricks I began to develop the ideas that I'm describing to you now in this book.
The correct honda weight for the Vertical Loop is the weight which balances the tensions in the spoke against those in the loop while it is spinning. When the spoke tension plus the outward force of the honda are equal to the loop tension, the diameter of the loop does not change. What we want to determine is the honda weight which keeps the loop diameter constant. I will now derive this weight using some basic laws from mechanical physics.
Figure 3.2 illustrates a blow-up of all the forces and tensions in the loop at and around the honda.
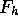 . Assuming that the honda is turning
with constant angular velocity,
. Assuming that the honda is turning
with constant angular velocity, 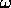 , the outward honda force is
, the outward honda force is
where 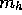 is the unknown honda mass and R is the
radius of the circle that the honda is moving in.
is the unknown honda mass and R is the
radius of the circle that the honda is moving in.
For a Vertical Loop, the angular velocity is not
constant, however, as a first order approximation
this is not too bad an assumption. Referring again to Figure 3.2,
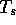 represents the spoke tension at the honda and
represents the spoke tension at the honda and
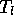 represents the loop tension. The spoke tension
must be equal to the outward force on the honda if the honda is to
continue in a circular path. Consequently, we have that
represents the loop tension. The spoke tension
must be equal to the outward force on the honda if the honda is to
continue in a circular path. Consequently, we have that
Furthermore, if the loop is to maintain a constant diameter we must have
Thus, if we knew the loop tension
we could calculate the honda mass as a function of 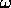 by substituting equations (3.2) and (3.3) into equation (3.1)
and solving for
by substituting equations (3.2) and (3.3) into equation (3.1)
and solving for 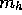
From equation (3.4) it appears that the honda mass is dependent on
the angular velocity, 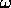 , of the loop. As you will see in what follows,
after the derivation of the loop tension, the term in
, of the loop. As you will see in what follows,
after the derivation of the loop tension, the term in 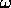 in equation (3.4)
conveniently disappears!
in equation (3.4)
conveniently disappears!
I now derive the loop tension by approximating the loop as
an equilateral geometric shape with N sides and then generalizing to
a circle by using a limiting argument. Thus, taking the total mass of
the loop to be 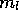 and distributing it over
N equally spaced points along a mass-less cord
we have, referring to the geometry in Figure 3.3, that the tension in
and distributing it over
N equally spaced points along a mass-less cord
we have, referring to the geometry in Figure 3.3, that the tension in
where 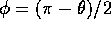 and
and 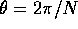 . Solving for
. Solving for 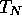 yields
yields
Now that an expression for 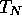 has been derived the loop tension,
has been derived the loop tension, 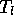 ,
is obtained simply by calculating the limit of
,
is obtained simply by calculating the limit of 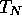 as
as 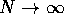 .
Since the limit of
.
Since the limit of 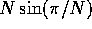 is
is  we have
we have
where the last equality comes from the fact that 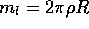 where
where 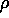 is the linear density of the cord. Plugging (3.7)
into (3.4) yields the correct honda mass for the Vertical Loop:
is the linear density of the cord. Plugging (3.7)
into (3.4) yields the correct honda mass for the Vertical Loop:
The result in (3.8) says that the honda mass which stabilizes the Vertical Loop is equal to the radius of the loop multiplied by the linear density of the cord. This a very simple and elegant result as well as a little surprising since we see that the required mass is independent of the speed at which the loop is turning!
 JPEG Image (28K)
JPEG Image (28K)